
Credit: Mike Zeng for Quanta Magazine.
In 1991, a group of physicists made an accidental discovery that flipped mathematics on its head. The physicists were trying to work out the details of string theory when they observed a strange correspondence: Numbers emerging from one kind of geometric world matched exactly with very different kinds of numbers from a very different kind of geometric world.
To physicists, the correspondence was interesting. To mathematicians, it was preposterous. They’d been studying these two geometric settings in isolation from each other for decades. To claim that they were intimately related seemed as unlikely as asserting that at the moment an astronaut jumps on the moon, some hidden connection causes his sister to jump back on earth.
“It looked totally outrageous,” said David Morrison, a mathematician at the University of California, Santa Barbara, and one of the first mathematicians to investigate the matching numbers.
Nearly three decades later, incredulity has long since given way to revelation. The geometric relationship that the physicists first observed is the subject of one of the most flourishing fields in contemporary mathematics. The field is called mirror symmetry, in reference to the fact that these two seemingly distant mathematical universes appear somehow to reflect each other exactly. And since the observation of that first correspondence — a set of numbers on one side that matched a set of numbers on the other — mathematicians have found many more instances of an elaborate mirroring relationship: Not only do the astronaut and his sister jump together, they wave their hands and dream in unison, too.
Recently, the study of mirror symmetry has taken a new turn. After years of discovering more examples of the same underlying phenomenon, mathematicians are closing in on an explanation for why the phenomenon happens at all.
“We’re getting to the point where we’ve found the ground. There’s a landing in sight,” said Denis Auroux, a mathematician at the University of California, Berkeley.
The effort to come up with a fundamental explanation for mirror symmetry is being advanced by several groups of mathematicians. They are closing in on proofs of the central conjectures in the field. Their work is like uncovering a form of geometric DNA — a shared code that explains how two radically different geometric worlds could possibly hold traits in common.
Discovering the Mirror
What would eventually become the field of mirror symmetry began when physicists went looking for some extra dimensions. As far back as the late 1960s, physicists had tried to explain the existence of fundamental particles — electrons, photons, quarks — in terms of minuscule vibrating strings. By the 1980s, physicists understood that in order to make “string theory” work, the strings would have to exist in 10 dimensions — six more than the four-dimensional space-time we can observe. They proposed that what went on in those six unseen dimensions determined the observable properties of our physical world.
“You might have this small space that you can’t see or measure directly, but some aspects of the geometry of that space might influence real-world physics,” said Mark Gross, a mathematician at the University of Cambridge.
Eventually, they came up with potential descriptions of the six dimensions. Before getting to them, though, it’s worth thinking for a second about what it means for a space to have a geometry.
Consider a beehive and a skyscraper. Both are three-dimensional structures, but each has a very different geometry: Their layouts are different, the curvature of their exteriors is different, their interior angles are different. Similarly, string theorists came up with very different ways to imagine the missing six dimensions.
One method arose in the mathematical field of algebraic geometry. Here, mathematicians study polynomial equations — for example, x2 + y2 = 1 — by graphing their solutions (a circle, in this case). More-complicated equations can form elaborate geometric spaces. Mathematicians explore the properties of those spaces in order to better understand the original equations. Because mathematicians often use complex numbers, these spaces are commonly referred to as “complex” manifolds (or shapes).
The other type of geometric space was first constructed by thinking about physical systems such as orbiting planets. The coordinate values of each point in this kind of geometric space might specify, for example, a planet’s location and momentum. If you take all possible positions of a planet together with all possible momenta, you get the “phase space” of the planet — a geometric space whose points provide a complete description of the planet’s motion. This space has a “symplectic” structure that encodes the physical laws governing the planet’s motion.
Symplectic and complex geometries are as different from one another as beeswax and steel. They make very different kinds of spaces. Complex shapes have a very rigid structure. Think again of the circle. If you wiggle it even a little, it’s no longer a circle. It’s an entirely distinct shape that can’t be described by a polynomial equation. Symplectic geometry is much floppier. There, a circle and a circle with a little wiggle in it are almost the same.
“Algebraic geometry is a more rigid world, whereas symplectic geometry is more flexible,” said Nick Sheridan, a research fellow at Cambridge. “That’s one reason they’re such different worlds, and it’s so surprising they end up being equivalent in a deep sense.”
In the late 1980s, string theorists came up with two ways to describe the missing six dimensions: one derived from symplectic geometry, the other from complex geometry. They demonstrated that either type of space was consistent with the four-dimensional world they were trying to explain. Such a pairing is called a duality: Either one works, and there’s no test you could use to distinguish between them.
Physicists then began to explore just how far the duality extended. As they did so, they uncovered connections between the two kinds of spaces that grabbed the attention of mathematicians.
In 1991, a team of four physicists — Philip Candelas, Xenia de la Ossa, Paul Green and Linda Parkes — performed a calculation on the complex side and generated numbers that they used to make predictions about corresponding numbers on the symplectic side. The prediction had to do with the number of different types of curves that could be drawn in the six-dimensional symplectic space. Mathematicians had long struggled to count these curves. They had never considered that these counts of curves had anything to do with the calculations on complex spaces that physicists were now using in order to make their predictions.
The result was so far-fetched that at first, mathematicians didn’t know what to make of it. But then, in the months following a hastily convened meeting of physicists and mathematicians in Berkeley, California, in May 1991, the connection became irrefutable. “Eventually mathematicians worked on verifying the physicists’ predictions and realized this correspondence between these two worlds was a real thing that had gone unnoticed by mathematicians who had been studying the two sides of this mirror for centuries,” said Sheridan.
The discovery of this mirror duality meant that in short order, mathematicians studying these two kinds of geometric spaces had twice the number of tools at their disposal: Now they could use techniques from algebraic geometry to answer questions in symplectic geometry, and vice versa. They threw themselves into the work of exploiting the connection.
Breaking Up Is Hard to Do
At the same time, mathematicians and physicists set out to identify a common cause, or underlying geometric explanation, for the mirroring phenomenon. In the same way that we can now explain similarities between very different organisms through elements of a shared genetic code, mathematicians attempted to explain mirror symmetry by breaking down symplectic and complex manifolds into a shared set of basic elements called “torus fibers.”
A torus is a shape with a hole in the middle. An ordinary circle is a one-dimensional torus, and the surface of a donut is a two-dimensional torus. A torus can be of any number of dimensions. Glue lots of lower dimensional tori together in just the right way, and you can build a higher dimensional shape out of them.
To take a simple example, picture the surface of the earth. It is a two-dimensional sphere. You could also think of it as being made from many one-dimensional circles (like many lines of latitude) glued together. All these circles stuck together are a “torus fibration” of the sphere — the individual fibers woven together into a greater whole.
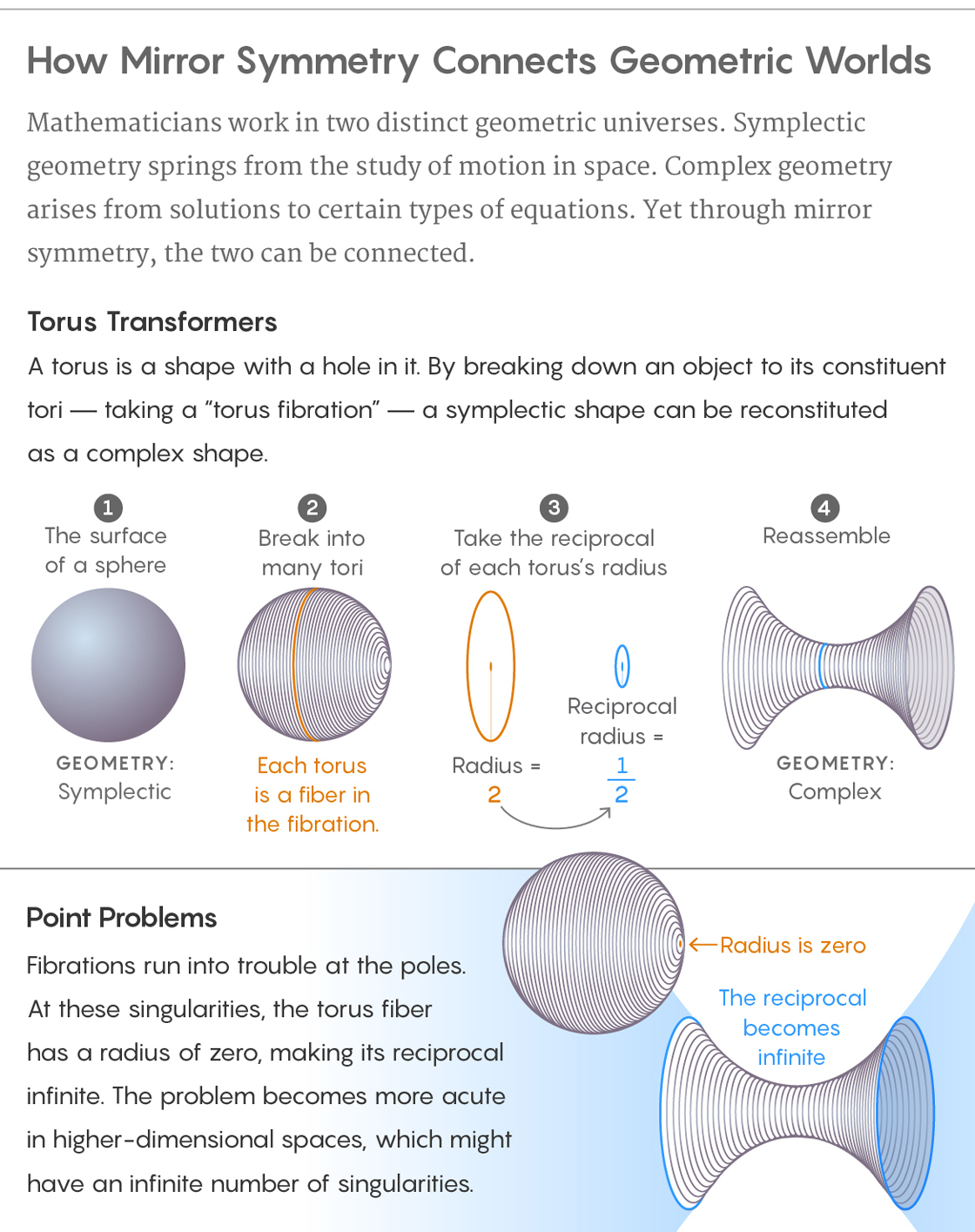
Credit: Lucy Reading-Ikkanda / Quanta Magazine.
Torus fibrations are useful in a few ways. One is that they give mathematicians a simpler way to think of complicated spaces. Just like you can construct a torus fibration of a two-dimensional sphere, you can construct a torus fibration of the six-dimensional symplectic and complex spaces that feature in mirror symmetry. Instead of circles, the fibers of those spaces are three-dimensional tori. And while a six-dimensional symplectic manifold is impossible to visualize, a three-dimensional torus is almost tangible. “That’s already a big help,” said Sheridan.
A torus fibration is useful in another way: It reduces one mirror space to a set of building blocks that you could use to build the other. In other words, you can’t necessarily understand a dog by looking at a duck, but if you break each animal into its raw genetic code, you can look for similarities that might make it seem less surprising that both organisms have eyes.
Here, in a simplified view, is how to convert a symplectic space into its complex mirror. First, perform a torus fibration on the symplectic space. You’ll get a lot of tori. Each torus has a radius (just like a circle — a one-dimensional torus — has a radius). Next, take the reciprocal of the radius of each torus. (So, a torus of radius 4 in your symplectic space becomes a torus of radius ¼ in the complex mirror.) Then use these new tori, with reciprocal radii, to build a new space.
In 1996, Andrew Strominger, Shing-Tung Yau and Eric Zaslow proposed this method as a general approach for converting any symplectic space into its complex mirror. The proposal that it’s always possible to use a torus fibration to move from one side of the mirror to the other is called the SYZ conjecture, after its originators. Proving it has become one of the foundational questions in mirror symmetry (along with the homological mirror symmetry conjecture, proposed by Maxim Kontsevich in 1994).
The SYZ conjecture is hard to prove because, in practice, this procedure of creating a torus fibration and then taking reciprocals of the radii is not easy to do. To see why, return to the example of the surface of the earth. At first it seems easy to stripe it with circles, but at the poles, your circles will have a radius of zero. And the reciprocal of zero is infinity. “If your radius equals zero, you’ve got a bit of a problem,” said Sheridan.
This same difficulty crops up in a more pronounced way when you’re trying to create a torus fibration of a six-dimensional symplectic space. There, you might have infinitely many torus fibers where part of the fiber is pinched down to a point — points with a radius of zero. Mathematicians are still trying to figure out how to work with such fibers. “This torus fibration is really the great difficulty of mirror symmetry,” said Tony Pantev, a mathematician at the University of Pennsylvania.
Put another way: The SYZ conjecture says a torus fibration is the key link between symplectic and complex spaces, but in many cases, mathematicians don’t know how to perform the translation procedure that the conjecture prescribes.
Long-Hidden Connections
Over the past 27 years, mathematicians have found hundreds of millions of examples of mirror pairs: This symplectic manifold is in a mirror relationship with that complex manifold. But when it comes to understanding why a phenomenon occurs, quantity doesn’t matter. You could assemble an ark’s worth of mammals without coming any closer to understanding where hair comes from.
“We have huge numbers of examples, like 400 million examples. It’s not that there’s a lack of examples, but nevertheless it’s still specific cases that don’t give much of a hint as to why the whole story works,” said Gross.
Mathematicians would like to find a general method of construction — a process by which you could hand them any symplectic manifold and they could hand you back its mirror. And now they believe that they’re getting close to having it. “We’re moving past the case-by-case understanding of the phenomenon,” said Auroux. “We’re trying to prove that it works in as much generality as we can.”
Mathematicians are progressing along several interrelated fronts. After decades building up the field of mirror symmetry, they’re close to understanding the main reasons the field works at all.
“I think it will be done in a reasonable time,” said Kontsevich, a mathematician at the Institute of Advanced Scientific Studies (IHES) in France and a leader in the field. “I think it will be proven really soon.”
One active area of research creates an end run around the SYZ conjecture. It attempts to port geometric information from the symplectic side to the complex side without a complete torus fibration. In 2016, Gross and his longtime collaborator Bernd Siebert of the University of Hamburg posted a general-purpose method for doing so. They are now finishing a proof to establish that the method works for all mirror spaces. “The proof has now been completely written down, but it’s a mess,” said Gross, who said that he and Siebert hope to complete it by the end of the year.
Another major open line of research seeks to establish that, assuming you have a torus fibration, which gives you mirror spaces, then all the most important relationships of mirror symmetry fall out from there. The research program is called “family Floer theory” and is being developed by Mohammed Abouzaid, a mathematician at Columbia University. In March 2017 Abouzaid posted a paper that proved this chain of logic holds for certain types of mirror pairs, but not yet all of them.
And, finally, there is work that circles back to where the field began. A trio of mathematicians — Sheridan, Sheel Ganatra and Timothy Perutz — is building on seminal ideas introduced in 1990s by Kontsevich related to his homological mirror symmetry conjecture.
Cumulatively, these three initiatives would provide a potentially complete encapsulation of the mirror phenomenon. “I think we’re getting to the point where all the big ‘why’ questions are close to being understood,” said Auroux.
Kevin Hartnett is a senior writer at Quanta Magazine covering mathematics and computer science.








