The other morning we were reading Verse 41 in the Tao Te Ching and came across this puzzling line:
"The Great Square has no corners"
which the Simple Explanation might tranlate as
"Ideal Squareness lacks corners"
Naturally, I began wondering about the Great Square with no corners and how Ideal Squareness would arise from the toroidal shape. After a couple of weeks of passive pondering and mental modeling, this is what I've come up with.
Since I'm accustomed to working with a 3-D mental model, I upped the square to a cube.
Then I imagined this cube suspended at its eight corner points against the inner walls of a spherical torus.
Here's an animated blue cube rotating inside a sphere I found on Google images. This will help to visualize what I'm talking about. The other Platonic shapes are rotating in there, too, but we will try to disregard them for now.

Of course, we want to imagine the sphere in the above link is a torus.
The center point of the cube would also be the center point of the torus. Now remove any lines, walls, or corners you may have imagined for the cube and just sense its pure Form suspended there, framed by the torus. This would be an Ideal Cube precisely placed in the only position a cube can occupy within the Ideal Torus. Perhaps this is the Great Square of the universal UC.
Now consider the following chalk drawings where I build the square and cube from two essential elements of the torus: the pole and the plane of the equator. This will give us another way of conceptualizing the Perfect Square and Perfect Cube.
 |
| This is a cross section of a torus. In the Simple Explanation, the white star at the middle is the transdimensional zero-point field from which creation springs forth. |
 |
| Torus with pole. There is only one line that goes straight up through the middle of a singularity or zero-point at the center of the torus without touching any curved sides. |
 |
| Torus with parallel poles, perpendicular to the equatorial plane, bisecting the toroidal tube. |
The chalk drawings below are the same series as the drawings above, but from a cutaway, topside view, looking straight down on the bottom half of the toroidal sphere from above.
| This is both a top-side cutaway view of the top and bottom planes of the perfect cube, and a side cutaway view of the perfect cube sitting in center of the toroidal tube. |
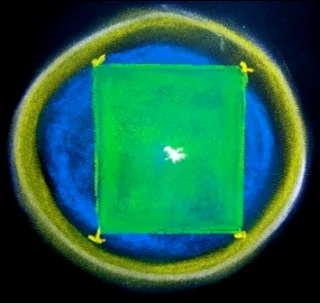 |
| This is also a view from the top of the plane of the equator radiating out from the center point until it bumps up against the inner walls of the confining toroidal space. |







I imagine this:
ReplyDeletehttp://img860.imageshack.us/i/cuadcircu10.png/
http://img30.imageshack.us/i/cuadcircu10inv.png/
a square spining that I can't see it just a circle. I have made some examples of this mandalas I would like to share with you, just tell me where to send to you, ok?
Hi Cesar. I went to imageshack and viewed the .png/ mandala images. Are those the ones you are speaking of?
ReplyDeleteYes, those images of the squares in the circle, spinning, work for this. I'm just taking that flat circle depicted at imageshack and making it a sphere (toroid actually) and turning the square(s) into a spinning cube in the center.
My google mail address is cyd.ropp@gmail.com but I hardly ever check it. Let me know if you send anything to gmail.
This article has been getting oodles views in the past two months. Is it Russian hackers, or what? Hard to believe this article is actually gaining any traction. Please, let me know if you are a human reading this comment. I doubt I'll get more than one or two comments, if that.
ReplyDeletecyd
i stumbled upon this page just because i am interested in toruses! not a russian hacker :)
DeleteGood to know. ;-) thanks for replying!
DeleteFound in 2024 pondering how a torus could be made out of other things like smaller toruses is an interesting one but I was wondering if the physical universe is a torus and it slides across a time line what would that look like
DeleteSome of us are working against the "Russian hackers!" Thanks for the info it adds to what I have been learning. Here is a quote by Galileo that you might like: The nature of existence] is written in that great book which ever is before our eyes... but we cannot understand it if we do not first learn the language and grasp the symbols in which it is written. The book is written in mathematical language, and the symbols are triangles, circles and other geometrical figures, without whose help it is impossible to comprehend a single word of it; without which one wanders in vain through a dark labyrinth. - Galileo
ReplyDeleteKeep on thinking this way - it will lead to miracles.
Thanks for your reply. I'm always singing that pretty song by the Indigo Girls about "Galileo, king of insight", to myself. Read my latest article about Gnostic Evolution--I have come to believe that DNA is literally that great book upon which "evolution" was written. It is ironic that science is finally coming around to proving the existence of God. It's there in our 90% "junk" DNA. Check it out.
DeleteThanks for this! Not a bot!
DeleteHa! Thanks for confirming your humanity! ;-) BTW, there's a nifty video on my Simple Explanation youtube site that demonstrates how that seed square in the middle of the red bell pepper rides freely within the skin of the pepper, much like a shock absorber. Look up Cyd Ropp, then Simple Explanation videos.
DeleteThis comment has been removed by the author.
ReplyDeleteI'm replying to a question above from Anonymous about the torus sliding through time. Here's an article of mine from 2022 that ponders that proposition: https://asimpleexplanation.blogspot.com/2022/07/a-simple-explanation-of-consciousness.html
ReplyDeletethe title of the post I just mentioned is called "A Simple Explanation of Consciousness and Time: Our Cherry-Jello Universe"
Delete