A Simple Explanation of Mirror Symmetry, the SYZ Conjecture, and Gravity

 An article in Quantum Magazine describes the problem with general relativity’s description of gravity:

General relativity yields the predictions of black holes and the Big Bang at the origin of our universe. Yet the “singularities” in these places, mysterious points where the curvature of space-time seems to become infinite, act as flags that signal the breakdown of general relativity. As one approaches the singularity at the center of a black hole, or the Big Bang singularity, the predictions inferred from general relativity stop providing the correct answers. A more fundamental, underlying description of space and time ought to take over. If we uncover this new layer of physics, we may be able to achieve a new understanding of space and time themselves.

I would like to offer a solution. According to the Simple Explanation cosmology, our universe is not shaped like a shuttlecock, as current theories propose, but rather like a donut—a torus. In this case, the  Big Bang occurred at the zero point singularity at the center of the cosmic torus and spread outward not as a sphere or a shuttlecock, but as an ever-expanding torus. Matter, as it emerges from the universal torus, forms itself into a steady stream of multi-dimensional toruses pushing out into the interior of the expanding 3-D donut, never reaching the edge which continues to grow beyond the reach of matter.

A newly emerging mathematical field called “mirror symmetry” demonstrates that there are an infinite number of toruses associated with every apparent object, looping themselves out of our ordinary 3-D space into six neighboring dimensions. An article printed in Quantum Magazine describes the “SYZ conjecture” this way:

 In the same way that we can now explain similarities between very different organisms through elements of a shared genetic code, mathematicians attempted to explain mirror symmetry by breaking down symplectic and complex manifolds into a shared set of basic elements called “torus fibers.”

A torus is a shape with a hole in the middle. An ordinary circle is a one-dimensional torus, and the surface of a donut is a two-dimensional torus. A torus can be of any number of dimensions. Glue lots of lower dimensional tori together in just the right way, and you can build a higher dimensional shape out of them.

To take a simple example, picture the surface of the earth. It is a two-dimensional sphere. You could also think of it as being made from many one-dimensional circles (like many lines of latitude) glued together. All these circles stuck together are a “torus fibration” of the sphere — the individual fibers woven together into a greater whole.

Here is the illustration of the concept provided by Quantum Magazine:

The Simple Explanation has always suggested that gravity is the force felt on the outside of ordinary objects due to presence of unseen toruses associated with ordinary matter. What the illustration refers to as “Point Problems” is actually the emergence of gravity. It seems to me that this symplectic geometry supplies a proof of this concept and, at the same time, resolves physic’s ongoing conundrum regarding the quantum level activity of black holes and the originating Bang.

We can imagine a very simple particle of matter as both that particle that we can see and measure and, at the same time, as a series of torus fibrations.  The fibrations at the poles with their infinite singularities originate the gravitational force, most of which occurs in alternate dimensions, but some of which “leaks” into our 3-D space. In the case of a small particle, the gravitational leakage is correspondingly small. But, when you aggregate particles into massive structures, the gravitational leakage becomes large and noticeable, as if the neighboring dimensions were trying to suck our space time into their dimensions.

The gravitational field around an object increases in proportion to the number of symplectic torus fibrations associated with the object’s ordinary matter. The reason gravity does not travel far from its originating object is because it is physically attached to the structure of the object—more precisely, to the toruses looping into neighboring dimensions. The more infinitely large singularities there are on the other side of the object’s multidimensional formula, the stronger the gravity of the object. The more aggregated ordinary matter, the more looping toruses.

In other words, gravity does not lead to black holes. Rather, massive objects produce so many toroidal fibrations of infinite singularities that the singularities themselves intrude into our 3-D space, revealing themselves and the toruses associated with them. When these singularities intrude into ordinary space, we see them in their normal symmetrical geometrical form as a single torus shape of infinite density and weight—a black hole.

Another conundrum standard physics is wrestling with has to do with “degrees of freedom.” Why, they wonder, do black holes have fewer degrees of freedom than ordinary objects? Meaning, why is their gravity only associated with the 2-dimensional outside surface of the black hole torus?

Since 2011, the Simple Explanation has suggested that gravity emanates from the exterior shell of the invisible torus wrapping around the exterior of ordinary matter.  In the case of a black hole, ordinary matter disappears into the center singularity, leaving only the shell of the symplectic torus to pull at space with its infinite gravitational shell, which is why the black hole’s gravity appears to be constrained  to the surface.

Top view of torus, with yellow arrows representing gravitational force

Side  view of torus, showing gravitational pull as well as material forces pushing out and wrapping around (white arrows)  From “Is Gravity a Toroidal Force?” 5-27-2011 Simple Explanation blog

I am grateful to Quantum Magazine for running these two recent articles on “Why Gravity Is Not Like the Other Forces” and “Mathematicians Explore Mirror Link Between Two Geometric Worlds.”  I believe “mirror symmetry” and the “SZY conjecture” provide the math behind the Simple Explanation’s theory of gravity. In symmetrical fashion, I hope my Simple Explanation will be discovered and considered by mathematicians and physicists struggling with these issues.

Reprint from Quanta Magazine: Mathematicians Explore Mirror Link Between Two Geometric Worlds

Here's a well-written article that explains how a toroidal universe is directly related to and mirrors our ordinary perceptions of space and geometry. In a nutshell, there are an infinite number of toruses associated with all ordinary geometric shapes. These toruses (aka tori) are situated in multi-dimensional space that is not perceived by our senses, but are nonetheless mathematically related to the objects that we can perceive. 

This newly discovered mathematical symmetry between ordinary perception and toroidal geometry fits in nicely with the Simple Explanation's model of toroidal realities. At this time, the mathematicians are able to make corresponding formulae that demonstrate the symmetry of these two vastly different geometries, but they are unable to explain the how or why. It is the how and why that the Simple Explanation cosmology provides, as yet undiscovered by conventional mathematicians and physicists. 

Curiously enough, this new symmetry is called the "SYZ conjecture" after the first initials of the 3-person team who discovered it, although the word "syzgy" means "yoked together," which is itself a highly appropriate title for this symmetrical geometry. Here's the reprinted article:

Decades after physicists happened upon a stunning mathematical coincidence, researchers are getting close to understanding the link between two seemingly unrelated geometric universes.

Quanta Magazine

• Kevin Hartnett

Credit: Mike Zeng for Quanta Magazine.

In 1991, a group of physicists made an accidental discovery that flipped mathematics on its head. The physicists were trying to work out the details of string theory when they observed a strange correspondence: Numbers emerging from one kind of geometric world matched exactly with very different kinds of numbers from a very different kind of geometric world.

To physicists, the correspondence was interesting. To mathematicians, it was preposterous. They’d been studying these two geometric settings in isolation from each other for decades. To claim that they were intimately related seemed as unlikely as asserting that at the moment an astronaut jumps on the moon, some hidden connection causes his sister to jump back on earth.

“It looked totally outrageous,” said David Morrison, a mathematician at the University of California, Santa Barbara, and one of the first mathematicians to investigate the matching numbers.

Nearly three decades later, incredulity has long since given way to revelation. The geometric relationship that the physicists first observed is the subject of one of the most flourishing fields in contemporary mathematics. The field is called mirror symmetry, in reference to the fact that these two seemingly distant mathematical universes appear somehow to reflect each other exactly. And since the observation of that first correspondence — a set of numbers on one side that matched a set of numbers on the other — mathematicians have found many more instances of an elaborate mirroring relationship: Not only do the astronaut and his sister jump together, they wave their hands and dream in unison, too.

Recently, the study of mirror symmetry has taken a new turn. After years of discovering more examples of the same underlying phenomenon, mathematicians are closing in on an explanation for why the phenomenon happens at all.

“We’re getting to the point where we’ve found the ground. There’s a landing in sight,” said Denis Auroux, a mathematician at the University of California, Berkeley.

The effort to come up with a fundamental explanation for mirror symmetry is being advanced by several groups of mathematicians. They are closing in on proofs of the central conjectures in the field. Their work is like uncovering a form of geometric DNA — a shared code that explains how two radically different geometric worlds could possibly hold traits in common.

Discovering the Mirror

What would eventually become the field of mirror symmetry began when physicists went looking for some extra dimensions. As far back as the late 1960s, physicists had tried to explain the existence of fundamental particles — electrons, photons, quarks — in terms of minuscule vibrating strings. By the 1980s, physicists understood that in order to make “string theory” work, the strings would have to exist in 10 dimensions — six more than the four-dimensional space-time we can observe. They proposed that what went on in those six unseen dimensions determined the observable properties of our physical world.

“You might have this small space that you can’t see or measure directly, but some aspects of the geometry of that space might influence real-world physics,” said Mark Gross, a mathematician at the University of Cambridge.

Eventually, they came up with potential descriptions of the six dimensions. Before getting to them, though, it’s worth thinking for a second about what it means for a space to have a geometry.

Consider a beehive and a skyscraper. Both are three-dimensional structures, but each has a very different geometry: Their layouts are different, the curvature of their exteriors is different, their interior angles are different. Similarly, string theorists came up with very different ways to imagine the missing six dimensions.

One method arose in the mathematical field of algebraic geometry. Here, mathematicians study polynomial equations — for example, x2 + y2 = 1 — by graphing their solutions (a circle, in this case). More-complicated equations can form elaborate geometric spaces. Mathematicians explore the properties of those spaces in order to better understand the original equations. Because mathematicians often use complex numbers, these spaces are commonly referred to as “complex” manifolds (or shapes).

The other type of geometric space was first constructed by thinking about physical systems such as orbiting planets. The coordinate values of each point in this kind of geometric space might specify, for example, a planet’s location and momentum. If you take all possible positions of a planet together with all possible momenta, you get the “phase space” of the planet — a geometric space whose points provide a complete description of the planet’s motion. This space has a “symplectic” structure that encodes the physical laws governing the planet’s motion.

Symplectic and complex geometries are as different from one another as beeswax and steel. They make very different kinds of spaces. Complex shapes have a very rigid structure. Think again of the circle. If you wiggle it even a little, it’s no longer a circle. It’s an entirely distinct shape that can’t be described by a polynomial equation. Symplectic geometry is much floppier. There, a circle and a circle with a little wiggle in it are almost the same.

“Algebraic geometry is a more rigid world, whereas symplectic geometry is more flexible,” said Nick Sheridan, a research fellow at Cambridge. “That’s one reason they’re such different worlds, and it’s so surprising they end up being equivalent in a deep sense.”

In the late 1980s, string theorists came up with two ways to describe the missing six dimensions: one derived from symplectic geometry, the other from complex geometry. They demonstrated that either type of space was consistent with the four-dimensional world they were trying to explain. Such a pairing is called a duality: Either one works, and there’s no test you could use to distinguish between them.

Physicists then began to explore just how far the duality extended. As they did so, they uncovered connections between the two kinds of spaces that grabbed the attention of mathematicians.

In 1991, a team of four physicists — Philip Candelas, Xenia de la Ossa, Paul Green and Linda Parkes — performed a calculation on the complex side and generated numbers that they used to make predictions about corresponding numbers on the symplectic side. The prediction had to do with the number of different types of curves that could be drawn in the six-dimensional symplectic space. Mathematicians had long struggled to count these curves. They had never considered that these counts of curves had anything to do with the calculations on complex spaces that physicists were now using in order to make their predictions.

The result was so far-fetched that at first, mathematicians didn’t know what to make of it. But then, in the months following a hastily convened meeting of physicists and mathematicians in Berkeley, California, in May 1991, the connection became irrefutable. “Eventually mathematicians worked on verifying the physicists’ predictions and realized this correspondence between these two worlds was a real thing that had gone unnoticed by mathematicians who had been studying the two sides of this mirror for centuries,” said Sheridan.

The discovery of this mirror duality meant that in short order, mathematicians studying these two kinds of geometric spaces had twice the number of tools at their disposal: Now they could use techniques from algebraic geometry to answer questions in symplectic geometry, and vice versa. They threw themselves into the work of exploiting the connection.

Breaking Up Is Hard to Do

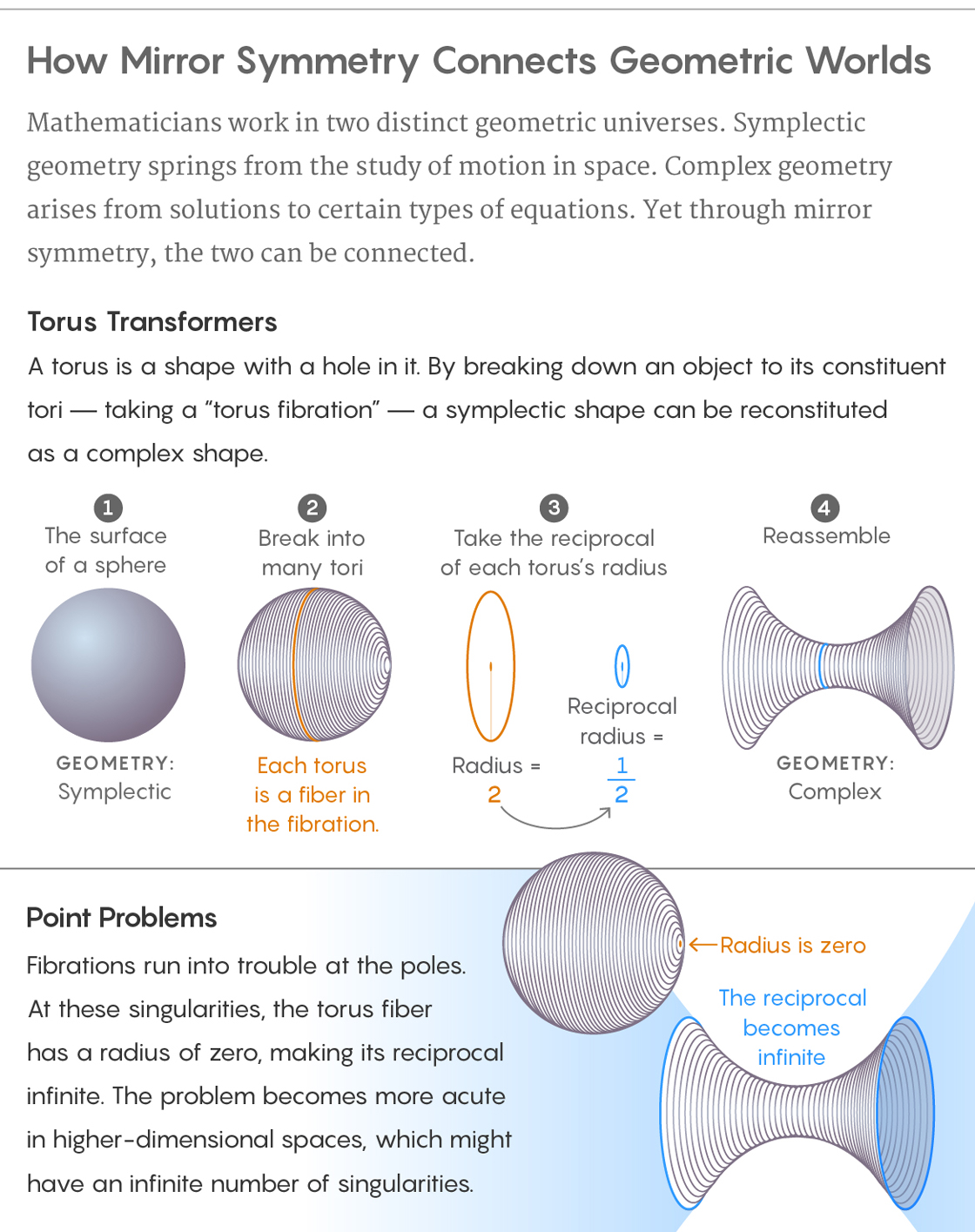
At the same time, mathematicians and physicists set out to identify a common cause, or underlying geometric explanation, for the mirroring phenomenon. In the same way that we can now explain similarities between very different organisms through elements of a shared genetic code, mathematicians attempted to explain mirror symmetry by breaking down symplectic and complex manifolds into a shared set of basic elements called “torus fibers.”

A torus is a shape with a hole in the middle. An ordinary circle is a one-dimensional torus, and the surface of a donut is a two-dimensional torus. A torus can be of any number of dimensions. Glue lots of lower dimensional tori together in just the right way, and you can build a higher dimensional shape out of them.

To take a simple example, picture the surface of the earth. It is a two-dimensional sphere. You could also think of it as being made from many one-dimensional circles (like many lines of latitude) glued together. All these circles stuck together are a “torus fibration” of the sphere — the individual fibers woven together into a greater whole.

Credit: Lucy Reading-Ikkanda / Quanta Magazine.

Torus fibrations are useful in a few ways. One is that they give mathematicians a simpler way to think of complicated spaces. Just like you can construct a torus fibration of a two-dimensional sphere, you can construct a torus fibration of the six-dimensional symplectic and complex spaces that feature in mirror symmetry. Instead of circles, the fibers of those spaces are three-dimensional tori. And while a six-dimensional symplectic manifold is impossible to visualize, a three-dimensional torus is almost tangible. “That’s already a big help,” said Sheridan.

A torus fibration is useful in another way: It reduces one mirror space to a set of building blocks that you could use to build the other. In other words, you can’t necessarily understand a dog by looking at a duck, but if you break each animal into its raw genetic code, you can look for similarities that might make it seem less surprising that both organisms have eyes.

Here, in a simplified view, is how to convert a symplectic space into its complex mirror. First, perform a torus fibration on the symplectic space. You’ll get a lot of tori. Each torus has a radius (just like a circle — a one-dimensional torus — has a radius). Next, take the reciprocal of the radius of each torus. (So, a torus of radius 4 in your symplectic space becomes a torus of radius ¼ in the complex mirror.) Then use these new tori, with reciprocal radii, to build a new space.

In 1996, Andrew Strominger, Shing-Tung Yau and Eric Zaslow proposed this method as a general approach for converting any symplectic space into its complex mirror. The proposal that it’s always possible to use a torus fibration to move from one side of the mirror to the other is called the SYZ conjecture, after its originators. Proving it has become one of the foundational questions in mirror symmetry (along with the homological mirror symmetry conjecture, proposed by Maxim Kontsevich in 1994).

The SYZ conjecture is hard to prove because, in practice, this procedure of creating a torus fibration and then taking reciprocals of the radii is not easy to do. To see why, return to the example of the surface of the earth. At first it seems easy to stripe it with circles, but at the poles, your circles will have a radius of zero. And the reciprocal of zero is infinity. “If your radius equals zero, you’ve got a bit of a problem,” said Sheridan.

This same difficulty crops up in a more pronounced way when you’re trying to create a torus fibration of a six-dimensional symplectic space. There, you might have infinitely many torus fibers where part of the fiber is pinched down to a point — points with a radius of zero. Mathematicians are still trying to figure out how to work with such fibers. “This torus fibration is really the great difficulty of mirror symmetry,” said Tony Pantev, a mathematician at the University of Pennsylvania.

Put another way: The SYZ conjecture says a torus fibration is the key link between symplectic and complex spaces, but in many cases, mathematicians don’t know how to perform the translation procedure that the conjecture prescribes.

Long-Hidden Connections

Over the past 27 years, mathematicians have found hundreds of millions of examples of mirror pairs: This symplectic manifold is in a mirror relationship with that complex manifold. But when it comes to understanding why a phenomenon occurs, quantity doesn’t matter. You could assemble an ark’s worth of mammals without coming any closer to understanding where hair comes from.

“We have huge numbers of examples, like 400 million examples. It’s not that there’s a lack of examples, but nevertheless it’s still specific cases that don’t give much of a hint as to why the whole story works,” said Gross.

Mathematicians would like to find a general method of construction — a process by which you could hand them any symplectic manifold and they could hand you back its mirror. And now they believe that they’re getting close to having it. “We’re moving past the case-by-case understanding of the phenomenon,” said Auroux. “We’re trying to prove that it works in as much generality as we can.”

Mathematicians are progressing along several interrelated fronts. After decades building up the field of mirror symmetry, they’re close to understanding the main reasons the field works at all.

“I think it will be done in a reasonable time,” said Kontsevich, a mathematician at the Institute of Advanced Scientific Studies (IHES) in France and a leader in the field. “I think it will be proven really soon.”

One active area of research creates an end run around the SYZ conjecture. It attempts to port geometric information from the symplectic side to the complex side without a complete torus fibration. In 2016, Gross and his longtime collaborator Bernd Siebert of the University of Hamburg posted a general-purpose method for doing so. They are now finishing a proof to establish that the method works for all mirror spaces. “The proof has now been completely written down, but it’s a mess,” said Gross, who said that he and Siebert hope to complete it by the end of the year.

Another major open line of research seeks to establish that, assuming you have a torus fibration, which gives you mirror spaces, then all the most important relationships of mirror symmetry fall out from there. The research program is called “family Floer theory” and is being developed by Mohammed Abouzaid, a mathematician at Columbia University. In March 2017 Abouzaid posted a paper that proved this chain of logic holds for certain types of mirror pairs, but not yet all of them.

And, finally, there is work that circles back to where the field began. A trio of mathematicians — Sheridan, Sheel Ganatra and Timothy Perutz — is building on seminal ideas introduced in 1990s by Kontsevich related to his homological mirror symmetry conjecture.

Cumulatively, these three initiatives would provide a potentially complete encapsulation of the mirror phenomenon. “I think we’re getting to the point where all the big ‘why’ questions are close to being understood,” said Auroux.

Kevin Hartnett is a senior writer at Quanta Magazine covering mathematics and computer science.

A Simple Explanation of Human Evolution and Reincarnation

 Occasionally one of my readers asks me questions that prompt great discussions. I treasure those interactions because it gives me the opportunity to share my understanding of these topics with others. 

This current article presents a series of questions asked this week by one such reader in the Comments section of a piece posted ten years ago called "Who Am 'I' After Death?" If you would like to read that short article first, this would put the following questions and answers into context.

Information, Evolution, and Reincarnation

Ruan has left a new comment on your post "Who Am "I" After Death?":

Hi Cyd,

I would be very interested to understand how the Simple Explanation might inform the mechanisms or processes of UC formation and specifically human population growth:

- Why/how is there such an exponential growth in human population on earth?

Humans enjoy sex. Sex creates the opportunity for UCs to recycle back to earth. Sex is a portal to earth.

- What drives the formation of more and more human UC’s?

All creatures on earth begin their evolutionary journey as simple, basic fractals of the Universal Unit of Consciousness (Universal UC). The humans did not start out as freshly minted humans. They began as single-celled creatures resembling prokaryotes about 4  billion years ago and worked their way up.

 

Later UCs continue to begin their earthly journeys as simple, single-celled creatures or as cellular components of more complex organisms. No one comes in directly as a human, except for the Christ figure who entered our timeline as a fully formed human being. (another topic—don’t get distracted)

- Is it just the continual karma/meme loop attempting to restore balance?

There is no balance to restore. Everything is going along and unfolding in time.

- If so, what would be the formation feedback loop to restore such balance as it seems to be continually growing out of control?

The humans are the alpha creatures on earth. UCs follow the “upward and onward” rule. The most ambitious UCs eventually graduate to humans and cluster there at the end of the evolutionary line because there is nowhere else to go.

- Where do the growing numbers of human UC’s come from?

The growing number of human UCs have acquired enough information to become humans. Not all UCs become humans. Most continue on as other life forms. There are many more other life forms on the planet than there are humans.

- Are they formed anew or are they further fractal breakdowns of prior human UC’s?

The karmic computer recycles the meme bundles of all creatures back into the most perfectly appropriate fit for the newly instantiated creature. A skin cell will most likely come back in as a skin cell because its meme bundle has become so good at the job of a skin cell. A bird will most likely come back as a bird because its meme bundle has gained so much knowledge as a bird that coming back as a bird is the best fit.  The dog will probably come back as a dog, and so on.

Your Self’s governing Unit of Consciousness, the part that you think of as yourself, is really only one UC out of the countless billions of UCs that form your body and work to keep you alive. When you die, your fractal unit of consciousness lets go of your personal meme bundle of information that you have acquired over countless lifetimes. That meme bundle will be recycled back into the most appropriate body available as it attaches to a newly fertilized egg in need of a soul. Then, as the embryo continues to develop, more and more UCs attach to the newly developing body as each cellular component and each new cell appears on the scene, each in need of their own UC. It is these UCs that know how to build and sustain the body, based upon their own personal histories and meme bundles. It is likely that most of the components of your body were also previously components of your body in previous lifetimes; for them, your body is the most perfectly appropriate place to reincarnate. This may explain the how and why of birth defects, as the cells reincarnate meme-based trauma from previous lifetimes. It also explains innate talents and abilities that children are born with.

It seems to me that when longstanding eco-systems are destroyed, the UCs of the displaced creatures are reincarnated elsewhere, wherever the karmic computer finds the most appropriate incoming body. Surely, displaced apes are able to graduate to human bodies and societies. For example, as a bonobo-inhabited forest is destroyed, the bonobo meme bundles attach to incoming human beings and that self then continues as a human. As wolf habitats are destroyed, the wolves reincarnate as dogs. As wild grasses are replaced by crops, the plants’ UCs reincarnate as rice and corn.

Every living thing on earth is composed of countless fractals of the Universal UC. That is their ultimate home. These earthly incarnations are transitory. There is no tragic loss of consciousness at the universal scale.

- What motivates/initiates/drives the point of inception of a new human UC?

The parents have sexual encounters with each other. Conception is a natural consequence of sex.

- Is it just the seemingly free will/choice of the “parents” of a human UC?

Yes.  Parents choose to have sex. Conception is out of their control, as it occurs at a cellular level.

- Is it just the natural forces of karma/memes causing some form of attraction forces?

I had an archetypal dream about 50 years ago that explains how and when meme bundles reattach themselves to UCs prior to reincarnating. You can read the Simple Explanation blog article here.

Here’s a snippet from the dream that tells, in metaphorical language how we pick up our meme bundles and dress our  UCs in them prior to reincarnating. Read the original article for the interpretation.

There is a young woman in the hut, sitting in a rocking chair nursing a baby, and they look a lot like the Madonna and Child. There is a box sitting on a crude, handmade table in the hut. I cross the room to look into the box and recognize my clothes are in there. I suddenly notice I am naked and I take my roughly hand-loomed tunic out of the box and put it on. Yes, this is mine. I turn and exit the hut. Rather than exiting into the village, the door out of the hut puts me directly back into the long, bright corridor.  I am near the end of the corridor now. I open and enter another door, and unexpectedly find myself outside the building, back out in the night air. 

 

To me, this dream implies that my UC was self-aware between lives. The setting was archetypal—mother; father; child; dwelling; corridors—all universal types of memes that apply equally to anyone. I was naked because my meme shroud of particulars had dropped away. When I looked into the box I recognized my meme shroud and was immediately inclined to put it on. The minute I reacquired my meme bundle, I found myself in the corridor and ejected back to earth.

- Is there a higher being/level/organization/force (e.g. “God” or “Higher Beings” etc.) driving/influencing/manipulating human UC formation or is the process just left up to itself?

Yes, there is the karmic computer, wielded by the Universal Unit of Consciousness. Or, if you prefer to consider this mechanism in religious terms, please visit my Gnostic Gospel blog and/or read The Gnostic Gospel Illuminated.

- How would all the above compare for non-human UC’s (i.e. the natural world of all other life forms on earth)?

The Simple Explanation of Absolutely Everything applies equally to all units of consciousness throughout the universe.

- From our scientific understanding of the natural world, there seems to be more direct/clear answers to the above, but the human UC’s seems to be exceptions or have a different set of rules?

Not necessarily, other than as explained above.  However, I happen to believe in the God Above God as described in my book, The Gnostic Gospel Illuminated.  I find the Gnostic view to be just as explanatory and more personally comforting for this existence I am now living. In the Gnostic Gospel, the metaversal consciousness is identified as The Father. The Universal Unit of Consciousness is The Son. The toroidal shape that surrounds our universe is the Waters, and the zero point field that emanates UCs into our space-time continuum is the birth canal of Sophia--The Mother of 10,000 Things. In Sophism, the earth is the fallen body of Logos, ruled by the Demiurge, mistakenly identified as “God,” by most religions.

- Is there a point of transition/progression from/between non-human UC’s and human UC’s?

Yes. It is based upon acquisition of information (memes) and readiness to perform as a human.

- What might be the rules or mechanisms of such transition, whether up or down or back or forth?

Units of consciousness operate under the Simple Explanation’s Golden Rule—All units of consciousness reach out to others like themselves to hold hands and work together to build things they cannot build alone. Skin cells hold hands to become the organ called skin. Organs hold hands to build organisms. Animals hold hands to build families and support societies. As this is a fractal, it works for all levels of instantiation.

When my housecat was stolen away and eaten by coyotes, her governing UC as the cat named Odot went out of this dimension until she was able to reincarnate as a kitten again. The UCs that made up her body were consumed by the coyote. Once inside the coyote, the UCs of the now non-functioning organs also departed to this dimension. But I think it’s possible that the UCs attached to the cat’s sub-cellular components carried on life as part of the coyote. This would be an example of lateral transfer of UCs from one creature to another, because the UCs of the organelles of a cat know how to carry on as organelles of a coyote. To them, it doesn’t much matter whose organelles they are, as long as they are still eukaryotes.

Perhaps when you eat a carrot, the UCs of the carrot are promoted to human component UCs and are able to reincarnate along with your human bundle of UCs.

- Would the above imply that there must also be similar (UC) life comparable to that on earth (i.e. “aliens”) elsewhere in the universe?

Not necessarily. Since the laws of the Simple Explanation are universal, everything described above can apply to any location within our universe.  On the other hand, it may be the case that our earth is a particular site of activity—a kind of consciousness laboratory that would make other locations redundant.  We’ll find out if/when the UFOs  land. 

We have come to the end of the questions. I hope this makes sense to you. You certainly asked the right questions!