Nested Rainbow Slinky Torus

Wow. Here's a pretty torus sculpture Gary and I just created.

Nested rainbow Slinky torus

Step one involves bending the Slinky around into a torus and securing the torus with a plastic connector. Figured that part out about a year ago.

This morning we took three different-sized Slinky's and stacked them.

Sorry this is sideways--can't get the darned picture to stay flipped!

Then we pushed the top two Slinky's down into the large rainbow-colored Slinky. Voila! Triple nested Slinky torus!

Nested Slinky torus sculpture by Cyd and Gary Ropp

There is a third Slinky nested inside the center. From the top it looks very much like a flower.

Here's a very cool one-minute video that shows all three Slinky's.

You would think that the Slinky toruses would have a difficult time nesting into each other, but the opposite is the case. It threaded itself perfectly as it clicked easily into place. You try it!

Three nested slinky's from the top.

I put the camera up against the outside Slinky and it looks like you're inside a giant torus! Magical!

Toroidal Symmetries and Fractal Divisions

Noodling around with a protractor, bisecting circles into smaller circles to make them into toroids. Along the way, the 2-D drawing displays beautiful symmetries of various kinds.

I drew this toroidal pattern using a pencil compass on paper. The lines you see at the circles' centers is where the compass dug into the paper. Pardon the mathematical imperfections, as this was done freehand.

I imported the drawing into Paint and airbrushed out the compass scratches. I can see toroids all over this drawing, but you may only be seeing the circles.

Here I've used the Paint program to highlight the largest torus in this drawing, which shows up if you imagine this as a cross-section of a sphere. The blue lines show the cross section of the torus cutaway. This inner torus has been subdivided again into two smaller tori (darker blue circles). The vertical yellow lines are the poles; the longest pole is for the central torus; the two shorter lines are the poles of the two subdivided tori. You can go on subdividing each torus this way, each time dividing the cutaway of the torus into half-sized tori.

This torus and its poles was used to illustrate "the great square within the torus." Same view as the blue lined cutaway above.

The darkest blue circles represent my clumsy eyeball method of illustrating how the torus is dividing fractally. Each torus cross section can divide into two more.
I wish I had a program that would draw these things more accurately. Any volunteers?

Notice the interesting way this fractal division works. It will go on forever, larger and larger or smaller and smaller, in true fractal manner.

Usually when I've thought about multiply-linked tori, they appear to nest at a single center pole, like Russian dolls. But these new drawings show how the tori can divide fractally along different lines. 

Concentric tori courtesy of http://www.multidimensionalmusic.com/review2.html

The Simple Explanation has also used nesting toroids to illustrate chakras.

 ******************************************

A little more fooling around in Paint gives us a "quasi torus" in the vertical direction (yellow). Look for more on this tie-in to quasi-particles in a future article.

Here I've used the poles to define a quasi torus perpendicular to the blue set. Following the logic of the Simple Explanation, I don't really think the tori divide up and down like this, along the poles, since the poles represent time and motion rather than space. I think the tori only divide in the horizontal (blue) space. But here we can see that this structure has room for a fully symmetrical set of divisions in the vertical (yellow) dimension.

The Great Square Within the Torus

The other morning we were reading Verse 41 in the Tao Te Ching and came across this puzzling line:

"The Great Square has no corners"

which the Simple Explanation might tranlate as

"Ideal Squareness lacks corners"

Naturally, I began wondering about the Great Square with no corners and how Ideal Squareness would arise from the toroidal shape. After a couple of weeks of passive pondering and mental modeling, this is what I've come up with.

Since I'm accustomed to working with a 3-D mental model, I upped the square to a cube.

Then I imagined this cube suspended at its eight corner points against the inner walls of a spherical torus. 

Here's an animated blue cube rotating inside a sphere I found on Google images. This will help to visualize what I'm talking about. The other Platonic shapes are rotating in there, too, but we will try to disregard them for now.

Click here to see the blue cube rotating inside a sphere.

Of course, we want to imagine the sphere in the above link is a torus.

The center point of the cube would also be the center point of the torus. Now remove any lines, walls, or corners you may have imagined for the cube and just sense its pure Form suspended there, framed by the torus. This would be an Ideal Cube precisely placed in the only position a cube can occupy within the Ideal Torus. Perhaps this is the Great Square of the universal UC.

Now consider the following chalk drawings where I build the square and cube from two essential elements of the torus: the pole and the plane of the equator. This will give us another way of conceptualizing the Perfect Square and Perfect Cube.

This is a cross section of a torus. In the Simple Explanation, the white star at the middle is the transdimensional zero-point field from which creation springs forth.



Torus with pole. There is only one line that goes straight up through the middle of a singularity or zero-point at the center of the torus without touching any curved sides.



Torus with pole and plane of equator. There is only one plane of the equator, which runs perpendicular to the pole and from side to side along the widest part of the torus, dividing the torus into top and bottom.

Torus with parallel poles, perpendicular to the equatorial plane, bisecting the toroidal tube.



Torus with perfect cube. The lines of the square/walls of the cube are precisely placed relative to the pole and equatorial plane. Once this shape is achieved within the torus, the Platonic shapes and all regular geometry are possible.

 

The chalk drawings below are the same series as the drawings above, but from a cutaway, topside view, looking straight down on the bottom half of the toroidal sphere from above.

   

Pardon my free-hand drawing. This is supposed to be a square touching the inside edge of the circle at four points, or a cube touching the inside edge of the torus at eight points. The center of the cube is the same as the center of the torus. All planes of the cube are either parallel or perpendicular to the pole and equatorial plane, thereby making the placement of this cube quite precise.



This is both a top-side cutaway view of the top and bottom planes of the perfect cube, and a side cutaway view of the perfect cube sitting in center of the toroidal tube.



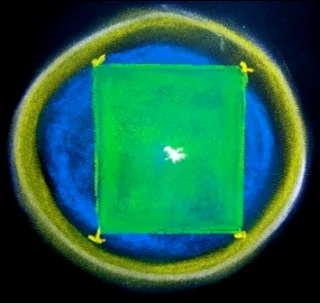This is also a view from the top of the plane of the equator radiating out from the center point until it bumps up against the inner walls of the confining toroidal space.



Here is the topside view of the torus, not cutaway. You can still see the white star at the middle from outside the torus looking down the funnel. The outside of this torus is white, just like the star at the middle, and the skin of the torus is feeding upward and wrapping over the lip of the funnel, then condensing toward the middle. At the middle, the outside metaversal energies turn inside out and push into the blue toroidal interior space, where material instantiates from energy and form.The funnel is barely visible; the white exterior is pouring up over the lip of the top of the torus and down into the funnel toward the ananada/joy zero point at the center.